ultra_dev
배열.격자판 최대합 본문
9. 격자판 최대합
설명
5*5 격자판에 아래롸 같이 숫자가 적혀있습니다.
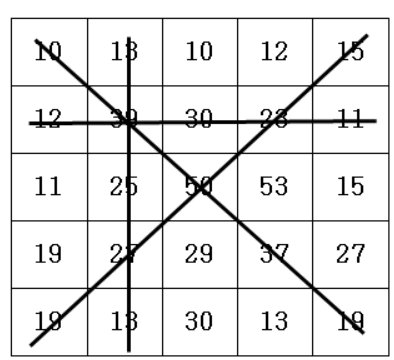
N*N의 격자판이 주어지면 각 행의 합, 각 열의 합, 두 대각선의 합 중 가 장 큰 합을 출력합니다.
입력
첫 줄에 자연수 N이 주어진다.(2<=N<=50)
두 번째 줄부터 N줄에 걸쳐 각 줄에 N개의 자연수가 주어진다. 각 자연수는 100을 넘지 않는다.
출력
최대합을 출력합니다.
예시 입력 1
5
10 13 10 12 15
12 39 30 23 11
11 25 50 53 15
19 27 29 37 27
19 13 30 13 19
예시 출력 1
155📌대각선[i][i], [i][n-1-i]
import java.lang.reflect.Array;
import java.util.*;
import java.util.Scanner;
class Main {
public int solution(int n, int[][] arr) {
//가장 큰 값을 넣어야하니 일단 작은 값으로 초기화
int answer = Integer.MIN_VALUE;
//sum1에는 행 sum2에는 열의 값을 합하겠음
//i가 0일때 j n까지 for문
// sum1은 앞에가 행번호 뒤에가 열번호[i][j]->행 고정후 열쪽 돌면서 행합계계산
//, sum2는 앞에가 열번호 뒤에가 행번호[j][i] 열 고정후 행쪽 돌면서 열합계계산
//포문하면 일단 sum1=sum2=0해서 0으로 초기화 하고 시작
//그래야 행,열별로 구해지면서 비교 가능하니
int sum1, sum2;
for (int i = 0; i < n; i++) {
sum1=sum2=0;
for (int j = 0; j < n; j++) {
sum1 += arr[i][j];
sum2 += arr[j][i];
}
answer = Math.max(answer,sum1);
answer = Math.max(answer,sum2);
}
//이제 대각선 [i][n-i-1]은 오른쪽부터 시작되는 대각선 구할때 왼쪽부터 시작되는 대각선은 [i][i]하면됨
sum1=sum2=0;
for (int i = 0; i < n ; i++) {
sum1 += arr[i][i];
sum2 += arr[i][n-1-i];
}
answer = Math.max(answer, sum1);
answer = Math.max(answer, sum2);
return answer;
}
public static void main (String[] args){
Main T = new Main();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] arr = new int[n][n];
for(int i = 0; i < n; i++){
for (int j = 0; j < n ; j++) {
arr[i][j] = sc.nextInt();
}
}
System.out.println(T.solution(n,arr));
}
}'알고리즘' 카테고리의 다른 글
| 배열.임시 반장 정하기 (0) | 2023.01.29 |
|---|---|
| 배열. 봉우리 격차 (0) | 2023.01.29 |
| 배열.등수 구하기 (0) | 2023.01.29 |
| 배열.점수계산 (0) | 2023.01.29 |
| 배열.뒤집은 소수 (0) | 2023.01.29 |
Comments
